一文带你吃透红黑树---红黑树如此简单
目录
目录
目录
作者有话说
二叉查找树
常见操作
查找(红黑树通用):查找每一个节点我们从根节点开始查找
插入:
查找最小值(红黑树通用):
查找最大值(红黑树通用):
查找前驱节点(红黑树通用):
查找后继节点(红黑树通用):
遍历(红黑树通用):
删除:
BST问题延续
AVL树
AVL树实现平衡
有了AVL树为什么还要红黑树呢?
构建一个AVL树的图示
左旋
右旋
2-3-4树
2-3-4树的构建过程
2-3-4树到红黑树转换规则
红黑树
定义
通过2-3-4树反对出红黑树的5大原则:
常见操作
变色:
左旋:
右旋:
新增:
删除(难点):
删除后的调整
总结描述:
红黑树视频参考:14-红黑树核心操作之-删除后调整-兄弟节点可借情况及代码实现_哔哩哔哩_bilibili
手写红黑树(代码)
作者有话说
想要玩转红黑树，要对模仿的玩法有一定的了解。我们在玩魔方时只要我们按照规则来，无论你的过程和步骤如何复杂或者如何简单，最后能够使每个面只要一种颜色结算成功。（杠精请离开：以3*3魔方为例）。玩红黑树也是一样的,只要按照规则(左旋、右旋、变色)来无论你中间的过程如何，最后都能写出红黑树(每一个人的步骤顺序可能不一样，其实原理都一样)。
电脑画图太费劲了，下面有一些图我就纸上画，望理解。有好的画图工具推荐的可以评论或私信哦。
找了很久的红黑树代码，没找到完整的。。。无奈之后自己写一份红黑树代码==>全网c++红黑树最全代码
二叉查找树
说起红黑树,首先得知道它的上古老祖: 二叉搜索树
定义:就是一颗二叉树，他的左节点比父节点小，右节点比父节点大。他的高度决定查找效率。
二叉搜索树是排序好的，应该说所有的二叉搜索树以及变种都是排序好的。怎么说，它是排序好的呢？以下能说明:二叉搜索树是基于二分的思想过来的,目的就是为了加快查找的效率。二分之前普遍要做的就是先排序，不可能对一个没有顺序的序列进行二分。
我们再来看下二叉搜索树排序的规则:当我们在一颗二叉搜索树的外围建立起一个坐标系,会发现一个神奇的现象。
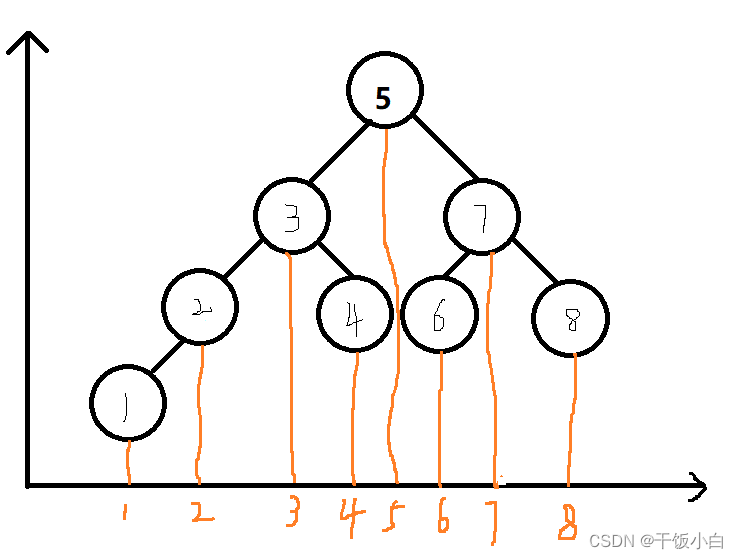
是不是,实际上就是在X坐标上排序的，然后进行的二分。包括我们所说的红黑树。
扩展:对于树的前序遍历、中序遍历、后序遍历的思考。无论是哪种便利，所有的访问顺序都一样只不过打印的时间不同而已。这个自己验证，哈。
常见操作
查找(红黑树通用):查找每一个节点我们从根节点开始查找
1.查找值比当前值大，则搜索右子树
2.查找值比当前值相等，则停止查找，返回当前节点
3.查找值比当前值小，则搜索左子树
插入:
要插入节点，必须先找到插入节点位置。依然是从根节点开始比较，小于根节点的话就和左子树比较，反之与右子树比较，直到左子树为空或者右子树为空，则插入到相应为空的位置。
查找最小值(红黑树通用):
沿着根节点的左子树一路查找，直到最后一个不为空的节点，该节点就是当前这个树的最大节点。
查找最大值(红黑树通用):
沿着根节点的右子树一路查找，直到最后一个不为空的节点，该节点就是当前这个树的最大节点。
查找前驱节点(红黑树通用):
小于当前节点的最大值
查找后继节点(红黑树通用):
大于当前节点的最小值
遍历(红黑树通用):
根据一定的顺序来访问整个树，常见的有前序遍历、中序遍历、后序遍历
删除:
本质上是找前驱节点或者后继节点来代替
有三种情况:
1.叶子节点直接删除
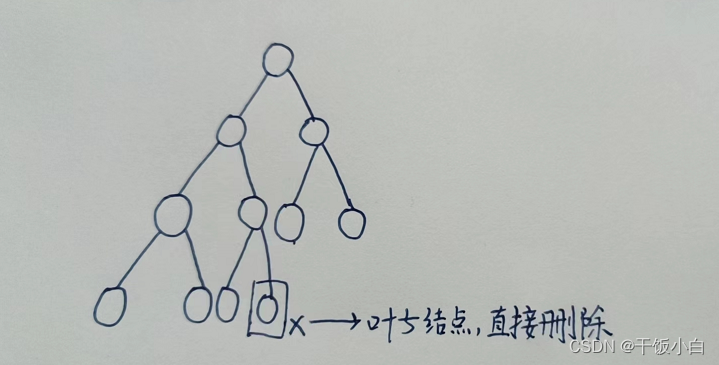2.只有一个子节点的用子节点代替
3.有两个子节点的，需要找到代替节点(前驱节点或者后继节点)
至于为什么要找前驱节点或者后继节点，我们回到二叉搜索树的定义：就是一颗二叉树，他的左节点比父节点小，右节点比父节点大。通过前驱节点和后继节点可以保持性质不变，后面在红黑树删除时也是通过这样的方式，不同的是红黑树需要保证黑色平衡，所以需要调整。
BST问题延续
我们回过头来说下二叉查找树的一个特殊情况:倾斜的二叉查找树，这棵树的高度为N
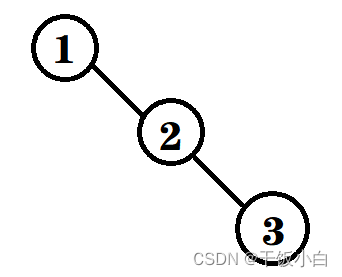
当我们顺序插入一组元素时就会出现二叉树退化成链表的情况，当退化成链表查找效率就变成了O(n)。
这里扩展说下O(n),O(logN)的差别有多大，我们画个函数曲线:
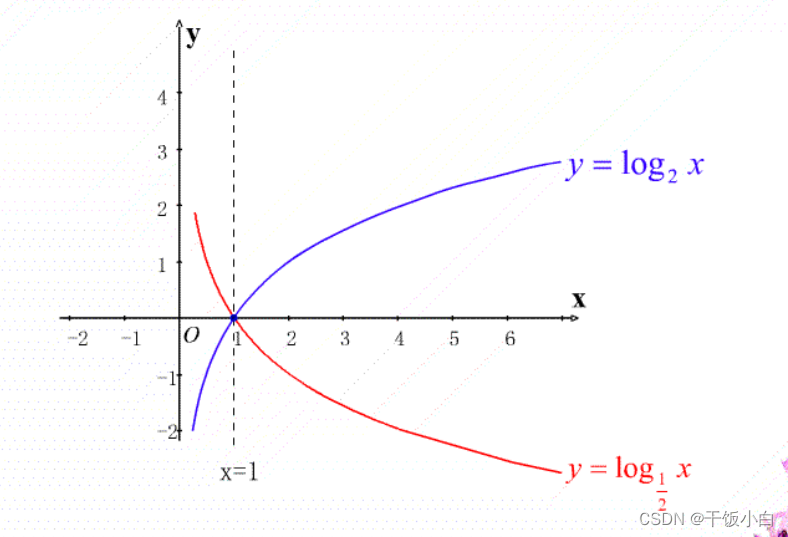
换句话说，大O表示法表述的是随着N的变化关系。所以我们在考虑是时候，要根据数据规模要考虑，当数据很少很少，用链表反而更快。
回到BST,基于BST存在的问题，平衡二叉查找树产生了。平衡树的插入和删除的时候会通过旋转操作将高度保持在logN，其中两款具有代表性的平衡树分别是AVL树(高度平衡具有二叉搜索树的全部性质，而且左右子树高度差不超过1)和红黑树。
如何选择AVL树还是红黑树:
当查找操作很多，几乎没有插入和删除操作，选择AVL树比红黑树效率更高。
当插入和删除操作比较多，选择红黑树比较合适。(你可以理解为:红黑树是低配折中方案)
AVL树
本来不是特别想说AVL树，既然写到这里就顺带说下，探究下AVL树为了保持平衡的需要的代价。高度平衡具有二叉搜索树的全部性质，而且左右子树高度差不超过1
AVL树实现平衡
通过左旋和右旋(说明下:左旋和右旋后一定不能破坏二叉查找树的查找规则)
有了AVL树为什么还要红黑树呢?
AVL树由于实现比较复杂，而且插入和删除性能比较差，在实际环境下的应用不如红黑树(红黑树只保持黑色节点平衡)。
构建一个AVL树的图示
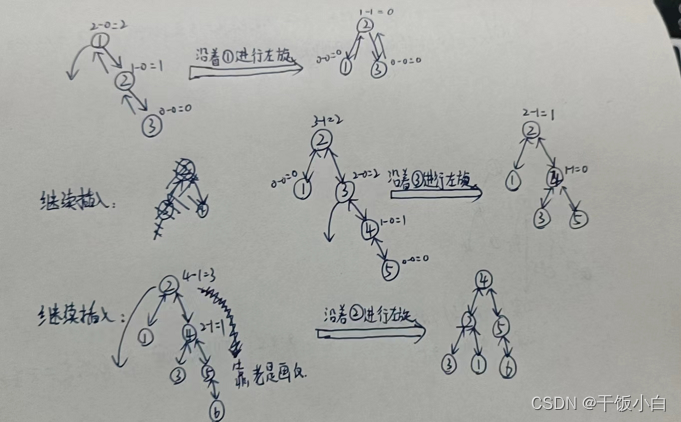
好像忘记提前说左旋、右旋操作了(很简单，代码也实现也简单)
左旋
怎么表示呢，怎么搞动图。我手画吧，写个例子
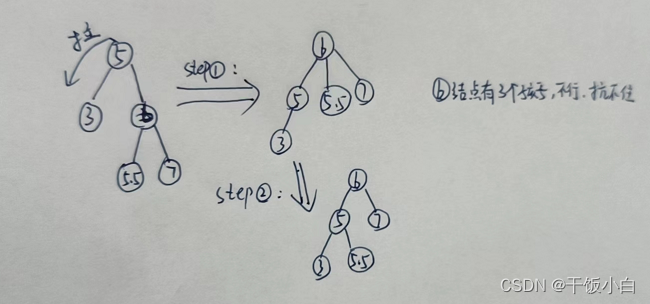
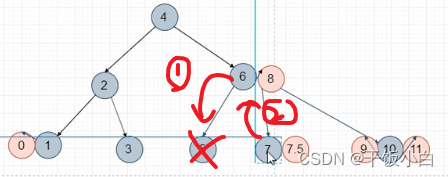
不晓得形象波？想象以下，有人沿着3-5-6这个线往下拉(想下定滑轮)，然5下去了，6上去了。此时5变成了6的子节点，6此时有3个子节点显然不符合二叉树，为了保持二叉查找树的基本性质，所以5.5变成5的右孩子最合适。
右旋
跟左旋相反，可以自己画图体会下。
2-3-4树
先说下，为什么要先写2-3-4树。因为2-3-4树的性质可以推导出红黑树的性质，听说红黑树是2-3-4树来了，不晓得是不是真的。反正方便我们理解红黑树是真的，当然要理解，总不能硬背吧，这样不方便根据实际情况进行优化，也容易忘记。
2-3-4树是四阶的B树(Balance Tree)，属于一种多路查找树，它的结构有以下限制。
1.所有叶子节点都拥有相同的高度(深度)
2.节点只能是2-节点，3-节点，4-节点之一
补充说明:
2-节点:其这个节点下面能挂载2个孩子
3-节点:其这个节点下面能挂载3个孩子
4-节点:其这个节点下面能挂载4个孩子
我们画图表示: 
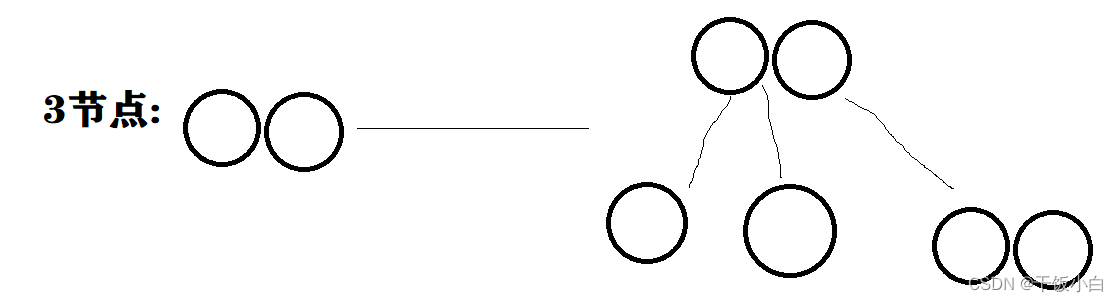
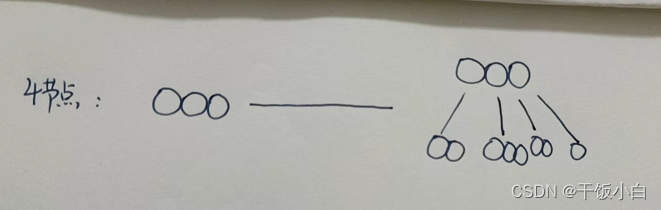
3.元素始终保持排序顺序，整体上保持二叉树的性质，即父节点大于左子节点，小于右子节点；而且节点有多个元素时，每个元素必须大于它左子树的元素。(纠正上图的错误:2-节点、3-节点、4-节点是一个整体)
看一个完整的2-3-4树:
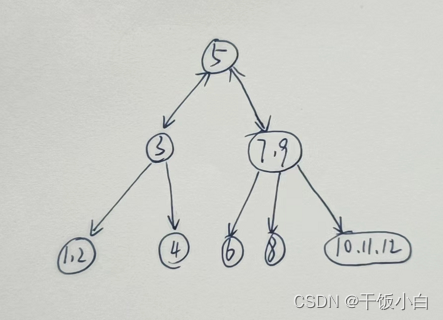
吐槽以下哈，写博客真正太不容易了。期待关注支持以下。。。。。
题外话:2-3-4树的查询操作像普通的二叉搜索树一样，非常简单，但是由于其结点元素数不确定，在一些编程语言中实现起来并不方便，实现一般使用它的等同-红黑树。一个2-3-4树可以对应多个红黑树，一个红黑树只能对应一个2-3-4树。
2-3-4树的构建过程
看图，值得注意的是分裂过程是向上的。也就是这个树的构建跟我们想象的不太一样，整棵树是向上生长的。
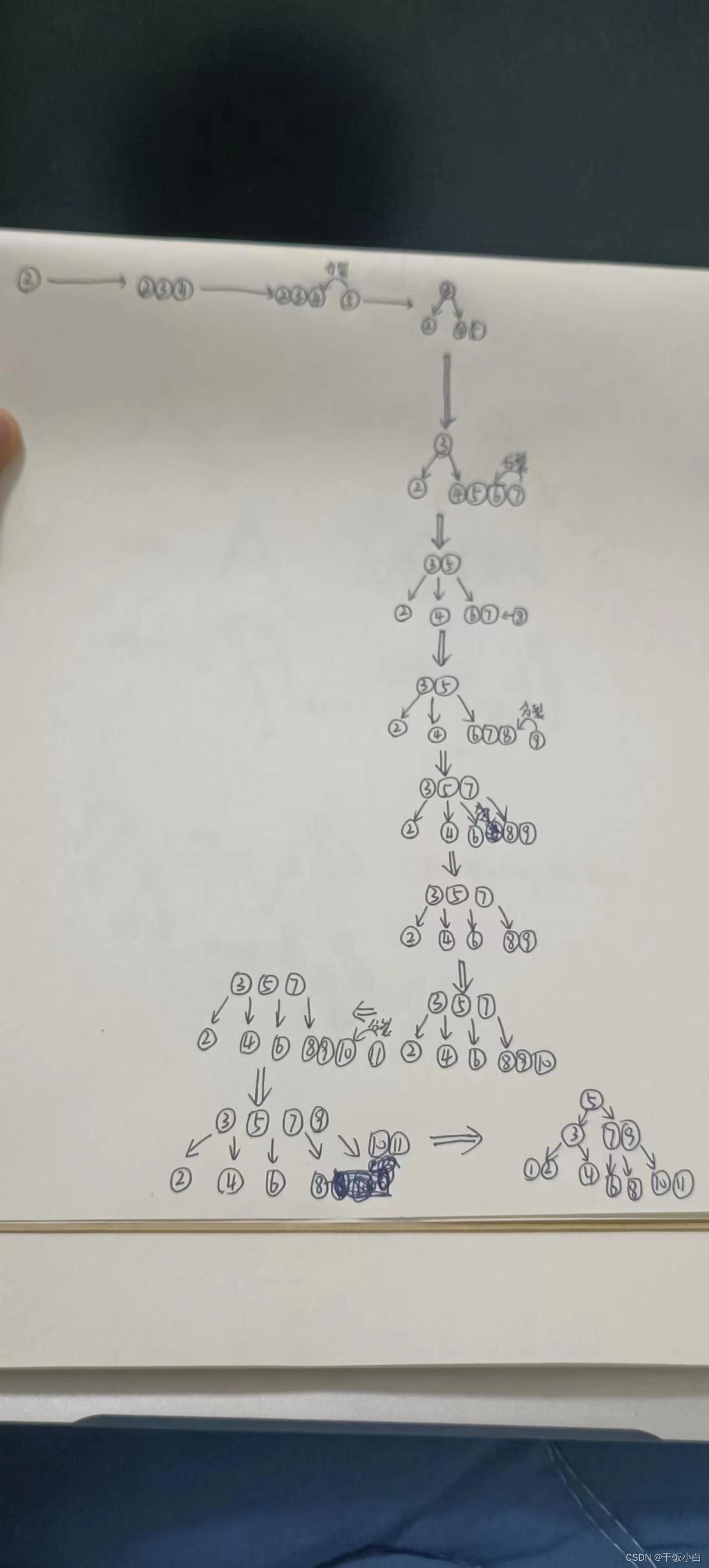
2-3-4树到红黑树转换规则
听说红黑树起源于2-3-4树，红黑树的本质是2-3-4树。不知道对不对，通过2-3-4树确实能够得到红黑树的5大规则。
重点:2-3-4树到红黑树的等级规则是重点，贯穿了整个接下来的内容。记住这四个等价关系，一会儿我们利用他们通过2-3-4树反推出红黑树的5大原则。
一共有4个等价关系:
2节点:
3节点:
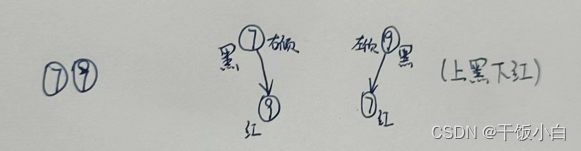
4节点:
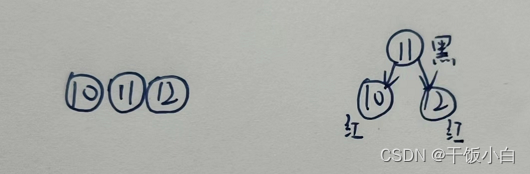
裂变关系:
通过上面的等级原则，将一个2-3-4树转换成红黑树:
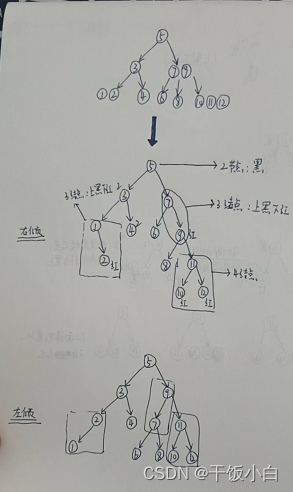
结论:一颗2-3-4树对应多个红黑树，一个红黑树只对应一个2-3-4树
红黑树
定义
红黑树是一种结点带有颜色属性的二叉查找树，但它在二叉查找树之外，还有以下5大性质:
1.节点是红色或者黑色
2.根是黑色
3.所有叶子都是黑色(叶子是NULL节点，这类节点不可以忽视)
4.每一个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
5.从任一节点到其每个叶子的所有简单路径的包含相同数目的黑色节点(黑色平衡)
下图就是一个典型的红黑树:
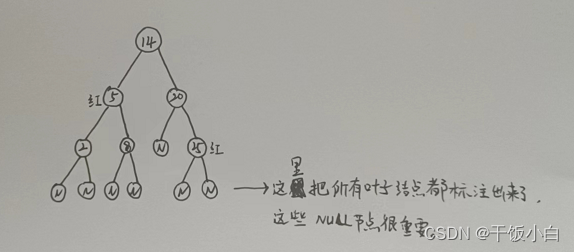
很多文章介绍红黑树到这里就结束了，其实这样是不方便我们真正理解红黑树的。我们需要去理解才能确保之后能够融汇贯通。
通过2-3-4树反对出红黑树的5大原则:
1.节点是红色或者黑色 ===> 不言而喻
2.根是黑色
这里需要分3中情况:根是2节点、根是3节点、根是4节点
2.1 根是3节点
2.1.0 
也就是这种情况，我们回顾下2-3-4树的3节点转化成红黑树的规则
2.1.1 2-3-4树的3节点对应红黑树转化: (上黑下红)
2.1.2 通过转化我们可以知道当2-3-4树的根是3节点时对应的红黑树的根一定是黑色
2.2 根是2节点
2.2.0 
也就是这种情况, 我们回顾下2-3-4树的2节点转化成红黑树的规则
2.2.1 2-3-4树的2节点对应红黑树转化:(直接转成黑色)
2.2.2 通过转化我们可以知道当2-3-4树的根是2节点时对应的红黑树的根一定时黑色
2.3 根是4节点
2.3.0 
也就是这种情况，我们回顾下2-3-4树的4节点转化成红黑树的规则
2.3.1 2-3-4树的4节点对应红黑树转化:(上黑下红)
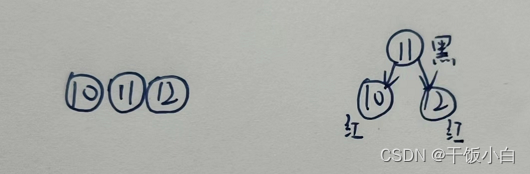
2.3.2 通过转化我们可以知道当2-3-4树的根是4节点时对应的红黑树的根一定时黑色
3.所有的叶子节点都是黑色 ===> 所有的2节点转化为红黑树都是黑色
4.每一个红色节点必须有两个黑色的子节点 ===> 为了保持黑色平衡(如规则5)
我们根据2-3-4树推出这个结论
4.1 当红色节点伪叶子节点(这里我们这么称呼是方便理解)
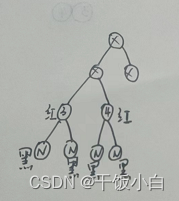
这种情况很好理解，我们回顾红黑树的规则3【所有叶子都是黑色(叶子是NULL节点，这类节点不可以忽视)】
4.2 先说明2-3-4树会发生裂变的情况，只有当2-3-4树的某个结点已经存在3个元素并且还需要往这个节点中插入新元素的时候，这时候就会向上发生分裂。
整个裂变的过程分成: 3节点转化--> 插入新节点(新插入的节点一定是红色) --> 判断是不是根节点(根节点需要变成黑色)。
5.从任一节点到其每个叶子的所有简单路径的包含相同数目的黑色节点
该规则也称之为黑色平衡，红黑树保持黑色平衡是很重要的性质。通过上述的一些规则有约定，我们可以发现我们构建的红黑树已经满足了黑色平衡。换句话说可能更加准确:红黑树只保持黑色平衡,不关注红色节点(这个性质在删除操作时会变现的很彻底)。正是因为红黑树的黑色平衡性质防止像二叉查找树一样退化成链表的情况，也减少了像AVL树为了保持高度平衡导致调整的代价太大。所以可以理解为AVL树的折中方案。
在实际的项目开发过程中，一味的选择红黑树作为底层的数据结构一定很合理嘛？答案显然不是,当我们的查找的次数远大于插入和删除的操作。我们可以选择AVL树，AVL树的高度平衡的特性在一定程度上比红黑树的高度要低，查找的效率更高。如果项目中的频繁的插入和删除操作那么就需要选择后红黑树,AVL为了保持高度平衡会付出很大的代价。
常见操作
我们介绍完了红黑树的5大规则，接下来我们看下红黑树的基本操作(左旋、右旋之前已经介绍过了，这里我们更详细介绍一次)。
变色:
节点的颜色由黑变红或者由红变黑
左旋:
以某一个节点作为旋转点，其右子节点变为旋转节点的父节点，右子节点的左子点变为旋转节点的右子节点，左子节点保持不变。
右旋:
以某一个节点作为旋转点，其左子节点变为旋转节点的父节点，左子节点的右子节点变为旋转节点的左子节点，右子节点保持不变。
新增:
分情况讨论，主要是要找到插入的位置，然后自平衡(左旋或者右旋)且插入节点是红色(如果是红色的话，那么当前分支上会多出一个黑色节点出来，从而破坏了黑色平衡)。
举例说明:以左子树为例子，右子树的情况则相反。
a.如果插入的是第一个节点(根节点)，红色变成黑色。
b.如果父节点为黑色，则直接插入，不需要变色。
c.如果父节点为红色，叔叔节点也是红色(此时爷爷节点一定是黑色)，则父节点和叔叔节点变黑色，爷爷节点变成红色(如果爷爷节点是根节点，则再变成黑色)，爷爷节点此时需要递归(把爷爷节点当作新插入的节点再次进行比较)
这里做个说明，为什么这种情况是爷爷一定是黑色的。在红黑树不可能存在两个连续的红色，因为红色节点一定是连着两个两个黑色的子节点的。
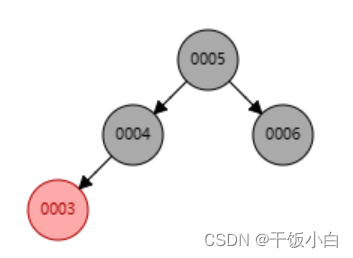插入3，因为5是根节点，需要再次变黑
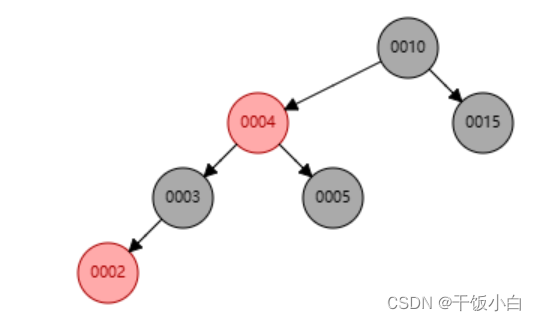
插入2，3和4变黑，4变红。满足黑色平衡，递归停止。
d.如果父节点是红色，没有叔叔节点或者叔叔节点是黑色(此时只能是NULL节点)，此时以爷爷节点为支点右旋，旋转之后原来的爷爷节点变红色，原来的父亲节点变黑色。
插入1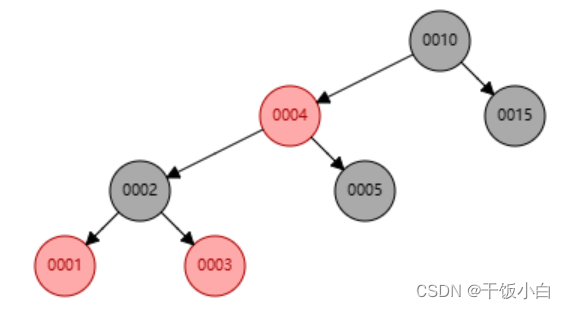 
不难看出，整个过程分成了两个部分:新增节点、新增之后的调整(见代码)
因为新增删除相对简单而且与删除操作类似，这里我们不详细介绍。我们重点看删除操作，弄懂删除操作，对于新增操作就自然明白了(还是不理解的朋友，可以留言或者私信一起讨论)。
删除(难点):
通俗点讲就是三句话 (大的情况分了三种)--> 自己能搞定的自己搞定、搞不定的找兄弟和父亲帮忙、父亲和兄弟都帮不了那有福同享，有难同当(父亲和兄弟自损节点)
其实删除和新增节点类似:删除节点、删除之后的调整(保持红黑树的规则)
我们详细的说下到底怎么删除才是合理的?
删除操作一共有三种情况：这三种情况根据红黑树节点情况进行划分的
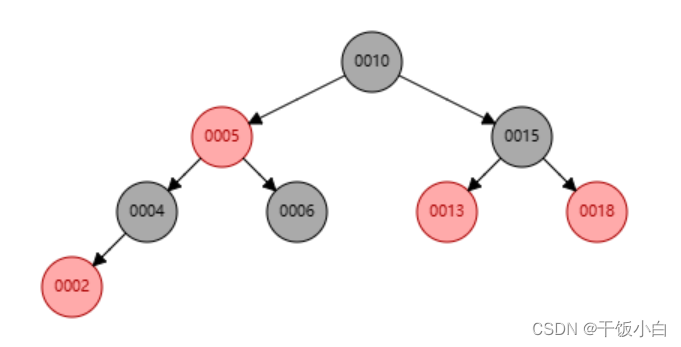
1.删除的是叶子节点，直接删除(例如: 删除2、6、13、18) --> 删除后仍然是颗红黑树
2.删除的节点有一个子节点，那么用子节点来替代删除节点(例如:删除4) --> 子节点替代后仍然是颗红黑树
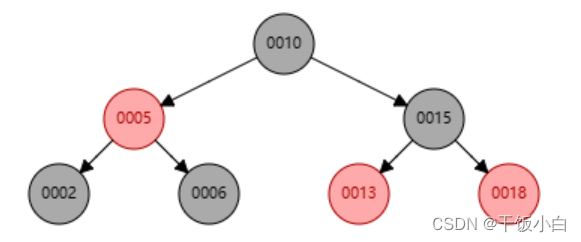
3.删除的节点有2个子节点，此时需要找到前驱节点或者后继节点来替代
这种情况比较复杂:我们通常是通过前驱节点或者后继节点来覆盖需要删除的节点，然后再将前驱节点或者后继节点删除。
为什么这么做呢?
比如上图:现在我们需要删除key = 10 的节点，如果直接删除 key = 10，那么需要将10断开，然后用key = 6，或者 key = 13去代替key = 10的位置，然后需要将 key = 6 或者 key = 13的节点删除。这样的代价显然比较大。
补充说明:前驱节点是小于当前节点的最大值、后继节点是大于当前节点的最小值
被删除的前驱节点或者后继节点只有2种情况:(回到了1、2的情况)
a.被删除节点是叶子节点
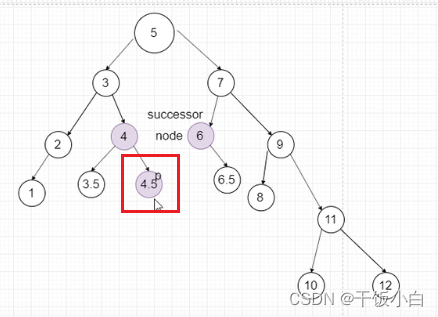
b.被删除节点只有一个孩(如下图的情况，要么是左孩子、要么是右孩子)
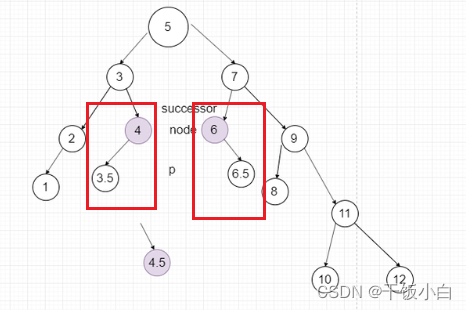
c.有一种特别的情况说明下，当只有一个根节点时直接删除即可(root = NULL)
删除后的调整
删除操作对应2-3-4树的关系
根据上面的解释，我们知道删除节点只能是叶节点或者带有一个子节点的非叶子节点。
我们接着分析: 红黑树的叶子节点和叶子节点的上一层一定对应2-3-4树的叶子节点，所以对应2-3-4树的删除，一定是删除2-3-4的叶子节点。【补充说明:2-3-4树是向上分裂的，所以2-3-4树是一个满二叉树，根据2-3-4树转化的红黑树非叶子节点以及非叶子节点的上以层以外的其他节点一定是有两个孩子的】
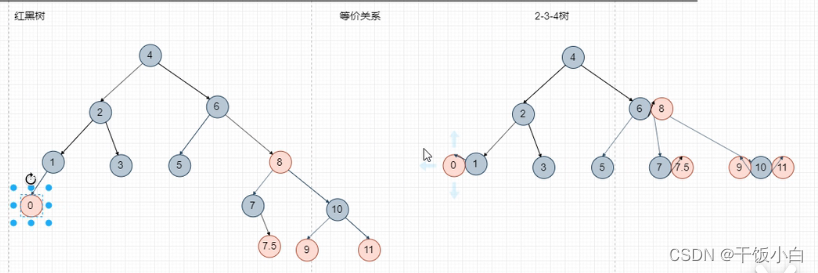
其实我们不难看出，2-3-4树本身就是保持黑色平衡的(2-3-4树没有颜色的,不要被误会了)
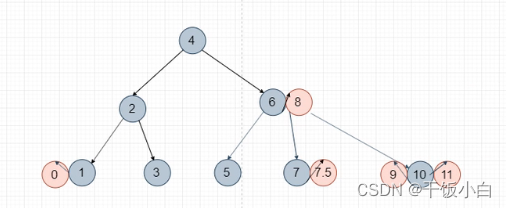
我们看下上面这张图，我们删除 0、1 、7、7.5、9、10、11都是合法的。说人话，在2-3-4树中我们删除3节点和4节点中的一个元素是合法的，删除后来仍然满足2-3-4树。
那我删除 key = 3、4、5呢? 当我们删除key=3时，key=2的节点需要挂两个孩子，不再满足时一颗2-3-4树。此时需要通过父节点向兄弟借，如果兄弟借不了，兄弟或者父亲节点用自己来借。
总结描述:
a.自己能搞定的自己搞定
- 如果删除的节点对应于2-3-4树的3节点或者4节点，则直接删除，不用跟兄弟和父亲节点借。
对应红黑树:如果删除的是红色节点，则直接删除。如果删除的是黑色节点，则红色节点上来替代，变黑即可，不需要调整。【红黑树删除情况的 1、2】
b.自己搞不定的找兄弟借，兄弟不借，找父亲借。父亲下来，兄弟找一个元素代替父亲【保证在x轴上的排序】
b.1 前提是找到"真正"的兄弟节点
b.2 兄弟有得借(此时兄弟节点一定是黑色，如果是红色那说明这个节点不是真正的兄弟节点，需要回到上一步找真正的兄弟节点)
兄弟节点有两个子节点的情况(2个子节点肯定是红色，如果是黑色的话相当于此时兄弟节点对应2-3-4树是2节点，不可能有多余的元素可以借)，此时需要旋转变颜色。
兄弟节点只有一个子节点的情况，此时需要旋转变色
c.父亲和兄弟自损节点
兄弟节点没有多余元素可借(此时兄弟节点一定是黑色2节点)，此时兄弟节点所在分支也要自损一个黑色节点以此达到黑色平衡，最快的方式就是兄弟节点直接变红(相当于就是减少一个黑色节点)，此时父亲节点为root的子树又达到了平衡(两边都比之前少一个黑色)。但是以祖父节点为root的树依然是不平衡的，此时需要递归处理。
手写红黑树
main.cpp ==> 用于测试
#include <iostream>
#include "RBTree.h"
using namespace std;
int main()
{
RBTree* tree1 = new RBTree();
int key = 0;
int value = 0;
// 插入
for(int i = 0; i < 10; i++)
{
key = i + 1;
value = i + 1;
tree1->put(key, value);
/*tree1->printTree();*/
}
// 删除
tree1->printTree();
while (1)
{
cin >> key;
tree1->remove(key);
tree1->printTree();
}
delete tree1;
return 0;
}RBTree.h
#pragma once
#define BLACK true
#define RED false
struct RBNode
{
RBNode* parent;
RBNode* left;
RBNode* right;
bool color;
int key;
int value;
RBNode()
{
}
RBNode(int key, int value, RBNode* parent)
{
this->key = key;
this->parent = parent;
this->value = value;
this->left = nullptr;
this->right = nullptr;
this->color = BLACK;
}
// 比较器
};
class RBTree
{
public:
RBTree():root(nullptr)
{
}
~RBTree()
{
}
// 新增
void put(int k, int v);
// 删除
int remove(int key);
// 打印
void printTree();
private:
// 左旋
void leftRotate(RBNode* p);
// 右旋
void rightRotate(RBNode* p);
// 新增调整
void fixAfterPut(RBNode* x);
// 寻找前驱节点
RBNode* predecessor(RBNode* node);
// 寻找后继节点
RBNode* sucessor(RBNode* node);
// 找到key对应的位置
RBNode* getNode(int key);
// 删除
void deleteNode(RBNode* node);
// 删除后调整
void fixAfterRemove(RBNode* x);
// 父节点
RBNode* parentOf(RBNode* node);
// 右孩子
RBNode* rightOf(RBNode* node);
// 左孩子
RBNode* leftOf(RBNode* node);
// 改变颜色
void setColor(RBNode* node, bool color);
// 获取颜色
bool colorOf(RBNode* node);
// 销毁红黑树
void deleteTree();
private:
RBNode* root;
};
RBTree.cpp
#include "RBTree.h"
#include <queue>
#include <iostream>
#include <stack>
/*
-----------------------------------------
围绕p左旋:
p r
/ \ / \
pl r ===> p rr
/ \ / \
rl rr pl rl
-----------------------------------------
*/
void RBTree::leftRotate(RBNode* p)
{
if (p != nullptr)
{
RBNode* r = p->right;
p->right = r->left;
if (r->left != nullptr)
{
r->left->parent = p;
}
r->parent = p->parent;
// 如果p是根节点
if (p->parent == nullptr)
{
root = r;
}
else if(p->parent->left == p) // p是左孩子
{
p->parent->left = r;
}
else // p是右孩子
{
p->parent->right = r;
}
r->left = p;
p->parent = r;
}
}
/*
------------------------------------------
围绕p右旋:
p pl
/ \ / \
pl r ===> p p
/ \ / / \
rl rr rl rr r
-----------------------------------------
*/
void RBTree::rightRotate(RBNode* p)
{
if (p != nullptr)
{
RBNode* l = p->left;
p->left = l->right;
if (l->right != nullptr)
{
l->right->parent = p;
}
l->parent = p->parent;
// 如果p是根节点
if (p->parent == nullptr)
{
root = l;
}
else if (p->parent->right == p) // p是左孩子
{
p->parent->right = l;
}
else // p是右孩子
{
p->parent->left = l;
}
l->right = p;
p->parent = l;
}
}
void RBTree::put(int k, int v)
{
RBNode* t = root;
// 如果是根节点
if (t == nullptr)
{
root = new RBNode(k, v, nullptr);
return;
}
// 需要插入位置
// 定义一个双亲指针
RBNode* parent = nullptr;
// 沿着跟节点寻找插入位置
do
{
parent = t;
if(k < parent->key)
{
t = t->left;
}
else if(k > parent->key)
{
t = t->right;
}
else
{
t->value = v;
return;
}
} while (t != nullptr);
// t == nullptr 说明没有找到相同的节点
RBNode* e = new RBNode(k, v, parent);
// 挂在左孩子上
if (k < parent->key)
{
parent->left = e;
}
else
{
parent->right = e;
}
// 调整
fixAfterPut(e);
}
/*
1. 2-3-4树：新增元素+2节点合并(节点中只有1个元素) = 3节点(节点中有2个元素)
红黑树:新增一个红色节点+黑色父节点 = 上黑下红 (不需要调整)
2. 2-3-4树: 新增元素+3节点合并(节点中只有2个元素) = 4节点(节点中有3个元素)
这里有6种情况:(左3、右3需要调整 | 左2右1、右2左1需要调整 | 其他2种情况不需要调整)
红黑树:新增一个红色节点+上黑下红 = 排序后中间节点是黑色,两边是红色(3节点)
3. 2-3-4树: 新增一个元素+4节点合并(节点中只有3个元素) = 原来的4节点分裂,中间元素升级为父节点，新增节点与剩下的节点合并
红黑树:新增一个红色节点+爷爷节点黑色,父节点和叔叔节点都是红色 = 爷爷节点变红,父亲和叔叔节点变黑,如果爷爷节点是根节点，则爷爷节点变黑
*/
void RBTree::fixAfterPut(RBNode* x)
{
x->color = RED;
// 如果父节点是黑色就不需要调整
while (x != nullptr && x != root && x->parent->color == RED)
{
//1.左3: x的父节点是爷爷的左孩子
if (parentOf(x) == leftOf(parentOf(parentOf(x))))
{
// 叔叔节点
RBNode* y = rightOf(parentOf(parentOf(x)));
// 如果叔叔节点是红色:情况3
if (colorOf(y) == RED)
{
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
}
else // 情况2
{
// 左2右1
if (x == rightOf(parentOf(x)))
{
RBNode* p = parentOf(x);
int tmpkey = p->key;
int tmpvalue = p->value;
p->key = x->key;
p->value = y->value;
x->key = tmpkey;
y->value = tmpvalue;
leftRotate(parentOf(x));
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rightRotate(parentOf(parentOf(x)));
}
}
else
{
// 叔叔节点
RBNode* y = leftOf(parentOf(parentOf(x)));
// 如果叔叔节点是红色:情况3
if (colorOf(y) == RED)
{
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
}
else // 情况2
{
// 左2右1
if (x == leftOf(parentOf(x)))
{
RBNode* p = parentOf(x);
int tmpkey = p->key;
int tmpvalue = p->value;
p->key = x->key;
p->value = y->value;
x->key = tmpkey;
y->value = tmpvalue;
rightRotate(parentOf(x));
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
leftRotate(parentOf(parentOf(x)));
}
}
}
root->color = BLACK;
}
RBNode* RBTree::predecessor(RBNode* node)
{
if (node == nullptr)
{
return nullptr;
}
if(node->left != nullptr)
{
RBNode* p = node->left;
while (p->right != nullptr)
{
p = p->right;
}
return p;
}
else
{
RBNode* p = node->parent;
RBNode* child = node;
while (p != nullptr && child == p->left)
{
child = p;
p = p->parent;
}
return p;
}
}
RBNode* RBTree::sucessor(RBNode* node)
{
if (node == nullptr)
{
return nullptr;
}
if (node->right != nullptr)
{
RBNode* p = node->right;
while (p->left != nullptr)
{
p = p->left;
}
return p;
}
else
{
RBNode* p = node->parent;
RBNode* child = node;
while (p != nullptr && child == p->right)
{
child = p;
p = p->parent;
}
return p;
}
}
int RBTree::remove(int key)
{
RBNode* node = getNode(key);
if (node == nullptr)
{
return -1;
}
int val = node->value;
deleteNode(node);
return val;
}
RBNode* RBTree::getNode(int key)
{
RBNode* node = root;
while (root != nullptr)
{
if (key < node->key)
{
node = node->left;
}
else if(key > node->key)
{
node = node->right;
}
else
{
return node;
}
}
return nullptr;
}
/*---------------------------------
删除操作:
1.删除叶子节点,直接删除
2.删除的节点有一个子节点,那么用子节点来替换
3.如果删除的节点有2个子节点，此时需要找到前驱节点或者后继节点来替代
-----------------------------------*/
void RBTree::deleteNode(RBNode* node)
{
// 3.node节点有2个孩子
if (node->left != nullptr && node->right != nullptr)
{
RBNode* sucessorNode = sucessor(node);
node->key = sucessorNode->key;
node->value = sucessorNode->value;
node = sucessorNode;
}
RBNode* replacement = node->left != nullptr ? node->left : node->right;
// 2.替代节点不为空
if (replacement != nullptr)
{
// 替代者的父指针指向原来的node的父亲
replacement->parent = node->parent;
if (node->parent == nullptr)
{
root = replacement;
}
else if(node == node->parent->left) // node是左孩子,所以替代者依然是左孩子
{
node->parent->left = replacement;
}
else // node是右孩子,所以替代者依然是右孩子
{
node->parent->right = replacement;
}
// 替换完之后需要调整平衡
if (node->color == BLACK)
{
// 需要调整，此时替代节点一定是红色(替代节点一定是红色,此时只要变色)
fixAfterRemove(replacement);
}
// 将node的左右孩子指针和父指针都指向null
node->left = node->right = node->parent = nullptr;
delete node;
}
else if(node->parent == nullptr) // 根节点
{
node->left = node->right = node->parent = nullptr;
delete node;
root = nullptr;
}
else // 1.叶子节点
{
// 调整
if (node->color == BLACK)
{
fixAfterRemove(node);
}
// 删除
if (node->parent != nullptr)
{
if (node == node->parent->left)
{
node->parent->left = nullptr;
}
else if(node == node->parent->right)
{
node->parent->right = nullptr;
}
// node->parent = nullptr;
node->left = node->right = node->parent = nullptr;
delete node;
}
}
}
void RBTree::fixAfterRemove(RBNode* x)
{
//情况2/3:
while (x != root && colorOf(x) == BLACK)
{
if (x == leftOf(parentOf(x)))
{
RBNode* rnode = rightOf(parentOf(x));
// 判断此时兄弟节点是不是真正的兄弟几点
if (colorOf(rnode) == RED)
{
setColor(rnode, BLACK);
setColor(parentOf(x), RED);
leftRotate(parentOf(x));
// 找到真正的兄弟节点
rnode = rightOf(parentOf(x));
}
// 情况3:兄弟没得借
if (colorOf(leftOf(rnode)) == BLACK && colorOf(rightOf(rnode)))
{
setColor(rnode, RED);
x = parentOf(x);
}
// 情况2:自己搞不定,需要向兄弟借,兄弟有得借
else
{
// 分两种小情况:兄弟节点本来是3节点或者4节点
if (colorOf(rightOf(rnode)) == BLACK)
{
setColor(leftOf(rnode), BLACK);
setColor(rnode, RED);
rightRotate(rnode);
rnode = rightOf(parentOf(x));
}
// 设置颜色
setColor(rnode, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(rnode), BLACK);
leftRotate(parentOf(x));
x = root;
}
}
else // x是右孩子
{
RBNode* lnode = leftOf(parentOf(x));
// 判断此时兄弟节点是不是真正的兄弟几点
if (colorOf(lnode) == RED)
{
setColor(lnode, BLACK);
setColor(parentOf(x), RED);
rightRotate(parentOf(x));
// 找到真正的兄弟节点
lnode = leftOf(parentOf(x));
}
// 情况3:兄弟没得借
if (colorOf(rightOf(lnode)) == BLACK && colorOf(leftOf(lnode)))
{
setColor(lnode, RED);
x = parentOf(x);
}
// 情况2:自己搞不定,需要向兄弟借,兄弟有得借
else
{
// 分两种小情况:兄弟节点本来是3节点或者4节点
if (colorOf(leftOf(lnode)) == BLACK)
{
setColor(rightOf(lnode), BLACK);
setColor(lnode, RED);
leftRotate(lnode);
lnode = leftOf(parentOf(x));
}
// 设置颜色
setColor(lnode, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(lnode), BLACK);
rightRotate(parentOf(x));
x = root;
}
}
}
//情况1:替代节点是红色,则直接染黑,补偿删除的黑色节点,这样红黑树依然保持平衡
//递归补偿
setColor(x, BLACK);
}
RBNode* RBTree::parentOf(RBNode* node)
{
return node != nullptr ? node->parent : nullptr;
}
RBNode* RBTree::rightOf(RBNode* node)
{
return node != nullptr ? node->right : nullptr;
}
RBNode* RBTree::leftOf(RBNode* node)
{
return node != nullptr ? node->left : nullptr;
}
bool RBTree::colorOf(RBNode* node)
{
// 如果为空,实际上是黑色
return node == nullptr ? BLACK : node->color;
}
void RBTree::setColor(RBNode* node, bool color)
{
if (node != nullptr)
{
node->color = color;
}
}
// 底层遍历
void RBTree::printTree()
{
std::queue<RBNode*> que;
que.push(root);
while (!que.empty())
{
RBNode* node = que.front();
que.pop();
if (node->color == RED)
{
std::cout << node->key << "(R)" << " ";
}
else
{
std::cout << node->key << "(B)" << " ";
}
if (node->left != nullptr)
{
que.push(node->left);
}
if (node->right != nullptr)
{
que.push(node->right);
}
}
}
void RBTree::deleteTree()
{
std::stack<RBNode*> sta;
std::queue<RBNode*> que;
while (!que.empty())
{
RBNode* node = que.front();
que.pop();
sta.push(node);
if (node->left != nullptr)
{
que.push(node->left);
}
if (node->right != nullptr)
{
que.push(node->right);
}
}
while (!sta.empty())
{
RBNode* tmp = sta.top();
sta.pop();
tmp->left = tmp->right = tmp->parent = nullptr;
delete tmp;
}
}